単回帰分析 - ROXX開発者ブログ

この記事は個人ブログと同じ内容です

www.ritolab.com

単回帰分析を学びます。

単回帰分析とは

データに基づき単一の説明変数と単一の目的変数の間の関係を定量化するために使用される統計手法。

例えば、2 つの変数 x と y の間の直線的な関係の強さを測る尺度として相関係数があるが、相関係数は二変数間に因果関係を前提とすることは無い。

これに対して、2 つの変数 x と y の間に何らかの因果関係を想定し、変数 x から変数 y の値を予測することを回帰分析という。

その回帰分析の中で、1 つの目的変数を 1 つの説明変数で予測するものが「単回帰分析」。

変数 x を説明変数・独立変数と呼ぶ
変数 y を被説明変数・目的変数・従属変数・応答変数と呼ぶ

また、直線の式 y = α + βx により予測する時、この直線を 回帰直線、α（アルファ）と β（ベータ）を 回帰係数 という。

回帰係数

回帰直線の式における α（アルファ）と β（ベータ）のこと。

回帰係数は測定の単位の影響を受ける。
- g（kg）で測った時の回帰係数 β は 1g (1kg) 増加した時の増加分を示す。

回帰直線

相関のある散布図において、データに最も当てはまりが良いように引いた直線。

この直線の式を構築することで単回帰分析を行う。

例題

ある乗り物に 10 〜 100 L の燃料を入れ走行距離を測定したところ以下の表の結果が得られた。この結果から、燃料の容量 x に対する走行距離 y を予測したい。

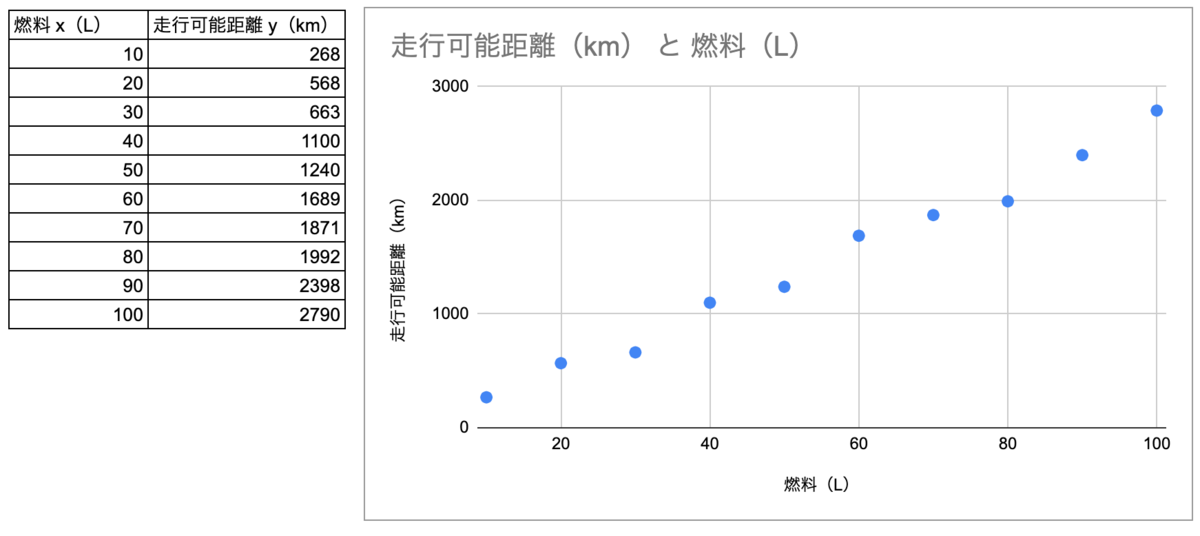
単回帰モデル

この散布図では、x と y に相関が見られるため、燃料の容量 x と走行距離 y の関係として、以下の直線の式があてはまると考えられる。

$\displaystyle y = α + βx$

α は y 切片で β は直線の傾き。

この直線が適切であれば、燃料の容量に対する走行可能距離が予測できる。

さらに、データから回帰係数 α と β の推定値 $\hat{α}$ と $\hat{β}$ が求まったなら、予測値 $\hat{y}$ も求めることができる。

つまり、この乗り物に 23 L の燃料を入れた時の走行距離は

$\displaystyle \hat{y} = \hat{α} + \hat{β}x$

に

x = 23 (L)

を代入すれば、予測値 $\hat{y}$ (km) が計算できる。

最小二乗法

最小二乗法は、回帰直線の回帰係数 α と β を推定する方法の 1 つ。

測定で得られた数値の組を、適当なモデルから想定される1次関数、対数曲線など特定の関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、残差平方和を最小とするような係数を決定する方法、あるいはそのような方法によって近似を行うことである。簡潔に言うと、誤差を伴う測定値の処理において、その誤差の二乗の和を最小にするようにし、最も確からしい関係式を求める方法である。
最小二乗法 - wikipedia

つまり、「データ個々に対する直線までの差」の二乗の総和を最小にするように求め回帰直線を選定していく方法。

掘り下げる

燃料の容量が $x_i$ (L) のときの走行距離は $y_i$ (km) (i=1,2,...,n)
i 番目の観測値 (x, y) に対して、予測値は $\hat{y}_i = \hat{α} + \hat{β}x_i$

残差

y に関する観測値 $y_i$ と予測値 $\hat{y}_i$ との間の差

$(y_i - \hat{y}_i)$

残差平方和

すべての観測値の残差 $y_i - \hat{y}_i$ （ i = 1, 2, ..., n）の平方和

$\displaystyle (y_1 - \hat{y}_1)^2 + (y_2 - \hat{y}_2)^2 + ... + (y_n - \hat{y}_n)^2 = \sum_{i=1}^{n}(y_i - \hat{y}_i)^2$

この残差平方和の式に $\hat{y}_i = \hat{α}$ と $\hat{β}x_i$ を代入する

$\displaystyle \begin{aligned} f(\hat{α}, \hat{β}) &= (y_1 -\hat{α} - \hat{β}x_1)^2 + (y_2 -\hat{α} - \hat{β}x_2)^2 + ... + (y_n -\hat{α} - \hat{β}x_n)^2 \\ &= \sum_{i=1}^{n}(y_i - \hat{α} - \hat{β}x_i)^2 \end{aligned}$

平方和であることから $f(\hat{α}, \hat{β}) ≧ 0$ であるため、残差の絶対値が大きいほど $f(\hat{α}, \hat{β})$ は大きな値になる。

-> この値を最小にするように回帰係数を決めていくのが最小二乗法。

最小二乗法を用いた回帰係数の推定値 $\hat{α}$ と $\hat{β}$ の求め方

回帰係数の推定値 $\hat{α}$ と $\hat{β}$ は、正規方程式と呼ばれる連立方程式の解として、次のように表す。

$\displaystyle \hat{β} = \frac{s_{xy}}{s^2_x} \biggl( = r_{xy} \frac{s_y}{s_x} \biggr), \quad \hat{α} = \bar{y} - \hat{β}\bar{x}$

それぞれを日本語に置き換えると、

$\hat{β}$ の求め方

$\displaystyle \hat{β} = \frac{x と y の共分散}{x の分散} \quad または\quad \hat{β} = x と y の相関係数 \biggl( \frac{y 標準偏差}{x 標準偏差} \biggr)$

$\hat{α}$ の求め方

$\displaystyle \hat{α} = y 平均値 - (\hat{β} × x 平均値)$

となる。

$\hat{β}$ が求まれば $\hat{α}$ も求められるので、回帰直線式を構築できる。

回帰直線を求める

実際に求めてみます。まずは $\hat{β}$ を求めるためにそれぞれの値を算出します。

$\displaystyle s^2_{x} = 825, \quad s_{xy} = 22457.5$

そして、 $\hat{β}$ を算出します。

$\displaystyle \hat{β} = \frac{22457.5}{825} = 27.22$

次に、 $\hat{α}$ を求めていきます。

$\displaystyle \bar{x} = 55, \quad \bar{y} = 1457.9$

$\hat{α}$ を算出します。

$\displaystyle \hat{α} = 1457.9 - (27.22 × 55) = -39.27$

よって、回帰直線式は以下になりました。

$\displaystyle y = -39.27 + 27.22x$

この回帰直線を先ほどの散布図に描画すると以下のようになります。

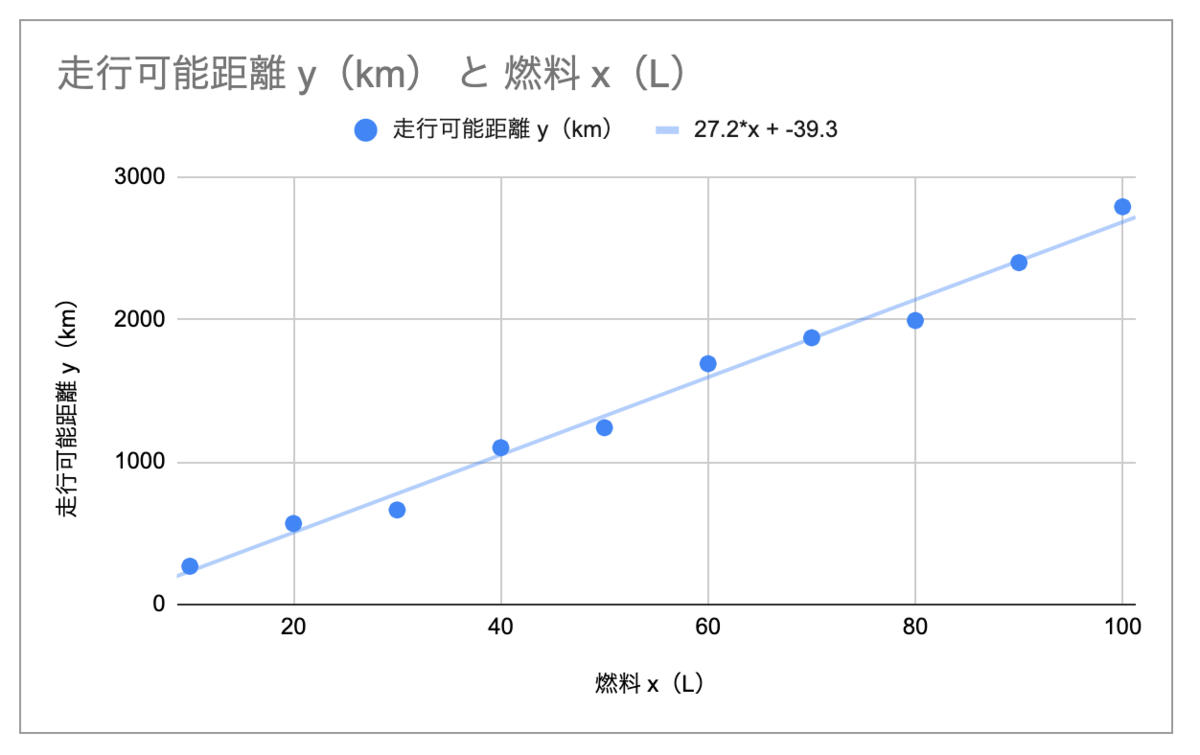
当てはまりの良さそうな直線に、最も確からしい関係式になっていそうです。

回帰直線式の使用

回帰直線式を構築できたので、実際に使ってみます。

23 L の燃料の場合の走行距離予測

$\displaystyle −39.27 + (27.22 × 23) = 586.86 km$

56 L の燃料の場合の走行距離予測

$\displaystyle −39.27 + (27.22 × 56) = 1485.12 km$

85 L の燃料の場合の走行距離予測

$\displaystyle −39.27 + (27.22 × 85) = 2274.5 km$

先ほどの散布図にこれらをプロットしてみると以下のようになります。

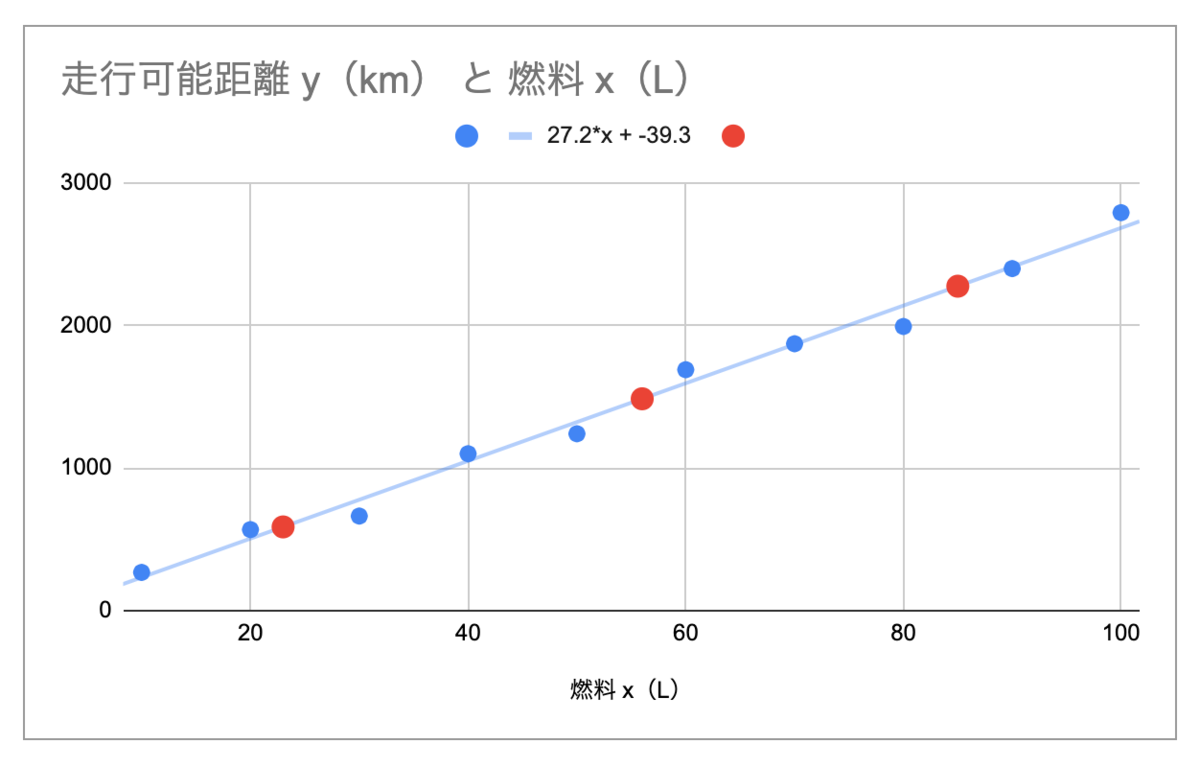
赤い点が予測した走行距離です。

回帰直線式にて導き出された走行距離が直線上に在るのがわかります。

単回帰分析から予測値を導出することができました。

回帰分析の注意点

回帰直線式から値を導いても、それはあくまでも「予測値」でしかないことを忘れてはいけない。
最小二乗法を用いているため、外れ値の影響を受ける。予めデータをよく確認し特殊例を除去する等の確認が必要。
二変数間の関係が直線的とみなせない場合、回帰直線ではなく 2 次曲線などの方が当てはまりが良いことがある。
複数のグループが混在している場合、グループごとに回帰直線を求める方が好ましい。
一般に、求められた回帰直線を用いて被説明変数 y から説明変数 x を予測してはいけない。
- y の残差に対する最小二乗法を用いて回帰直線が導出されるため
- つまり、x から y を予測するのみで使え。ということ
与えられたデータが存在する範囲から大きく離れている値 x に対しては、直線的な関係が成立しない可能性があるので、単純に予測に利用してはいけない。
- 離れた値を回帰分析の x に代入し予測値を求めることを「外挿」といい、外挿は避けるべきとされている。
- 例えば今回の例題では「燃料の容量 10 〜 100 L に対する走行距離」が測られているが、燃料 1000 L ではこの関係が利用できるかどうかは保証されず、この式で走行距離を予測すべきではない。ということ。

python で実行

python で単回帰分析を実装してみます。

scikit-learn を使っています。

import os
import pandas as pd
from sklearn import linear_model

dirname = os.path.dirname(__file__)
dataPath = dirname + '/data.csv'

df = pd.read_csv(dataPath)

clf = linear_model.LinearRegression()

# 説明変数
X = df[['燃料']]

# 目的変数
Y = df[['走行距離']]

# モデル作成
clf.fit(X, Y)

# 回帰係数
print('回帰係数: ', clf.coef_)

# 切片
print('切片: ', clf.intercept_)

# 決定係数
print('決定係数: ', clf.score(X, Y))


# モデルを使用して予測
# 23L, 56L, 85L の場合で予測する
data = {
    '燃料': [23, 56, 85]
}
d = pd.DataFrame(data)

# 予測
result = clf.predict(d)


print('結果', result)

実行結果

回帰係数:  [[27.22121212]]
切片:      [-39.26666667]
決定係数:  0.9887399026294627

結果:  [
 [586.82121212]
 [1485.12121212]
 [2274.53636364]
]

回帰係数、切片ともに手計算したものと同じ。
決定係数が高いので、当てはまりは良い。
- 今回のデータは観察結果ではなくサンプルで作ったデータというのもあり決定係数が高い。
予測結果も意図通り出ている。

かねがね良さそうです。

Jupyter Notebook で描画してみます。

import matplotlib.pyplot as plt
import seaborn

# 観察データ描画
plt.scatter(X, Y)
 
# 回帰直線
plt.plot(X, clf.predict(X))

# 予測値をプロット
plt.scatter(d, result)

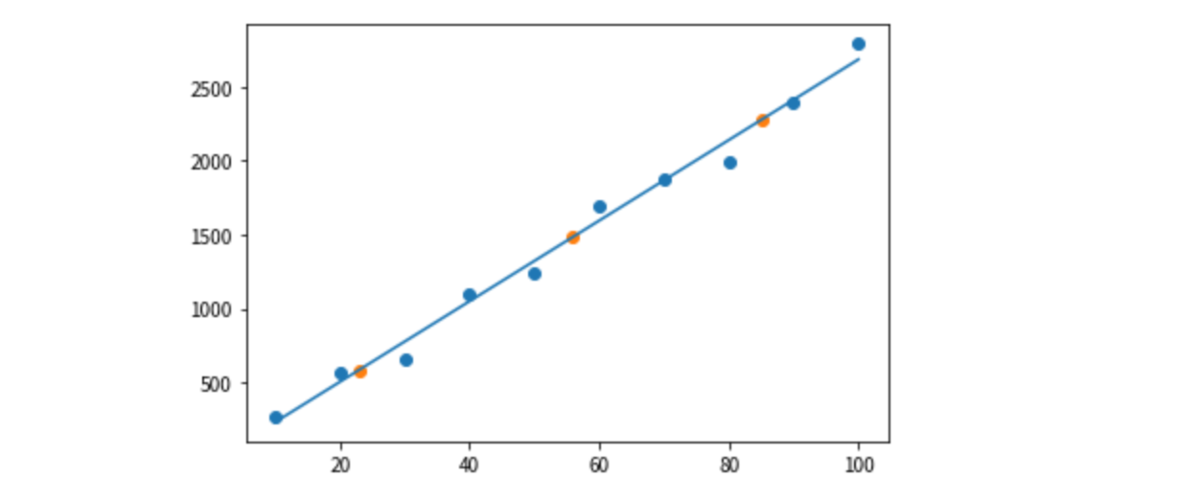
手計算のものと同じになりました、こちらも良さそうです。

現在 back check 開発チームでは一緒に働く仲間を募集中です。

herp.careers