重回帰分析におけるモデルの構築と評価

この記事は個人ブログと同じ内容です

www.ritolab.com

重回帰分析における機械学習・モデルの構築を行い、モデルの検査・精度評価までを行なっていきます。本記事は学習と実践の記録です。

重回帰分析とは

目的変数を、複数の説明変数によってどれだけ説明できるかを定量的に分析する手法。

基本的には、目的変数、説明変数ともに定量データである際に用いる。

概ね分析結果を以下のように使える

複数説明変数から目的変数を推定する式を作成し予測に活用。
目的変数に対する説明変数それぞれの影響度合いを見る。
- 推定したい値の決定に、それぞれの項目がどれだけ影響を及ぼしているのか。

今回は前者を行っていく。

scikit-learn のアルゴリズムチートシート

線形重回帰モデル

例えば賃貸マンションのデータでは、家賃を説明する変数として面積、築年数、駅徒歩（最寄り駅から徒歩で何分かかるか）などが考えられる。

複数（p）個の説明変数を用いる線形重回帰モデルを考えると以下の式になる

$\displaystyle y_i = β_0 + β_1x_{1i} + ... + β_px_{pi} + ε_i, \quad (i = 1, 2, ..., n)$

説明変数が 3 つの時

$\displaystyle y_i = β_0 + β_1x_{1i} + β_2x_{2i} + β_3x_{3i} + ε_i$

$β_0$ : 切片
β1 ,..., βp : 偏回帰係数
- 重回帰分析における説明変数の回帰係数
  - 説明変数を標準化（平均 0, 分散 1）した場合は標準偏回帰係数となる
: 誤差項
- 「回帰モデル内に含まれていない要因に起因するバラツキ」を表すもの
- 互いに独立で、正規分布 $N(0,σ^2)$ に従う。

総和記号を使って表現

$\displaystyle y = \sum_{p=1}^{p} β_px_{pi} + b$

誤差項（error term）について

賃貸マンションの家賃推定のモデル構築に面積・築年数・駅徒歩を使ったとして、実際の家賃の決定にはこれ以外にも要因があり（土地の地価や設備、ペット可否など）それらにも左右されるためデータは回帰直線に対して完全には一致しない。
そのため基本的な関係は回帰直線上にあると考え他の要因については予測できない確率的なものだと考えることにし、この「予測できない部分」を 誤差項という。

例題

「とある地域の賃貸マンションにおける家賃の推定」を線形重回帰モデルを作成し実施していきます。

目的変数を「家賃」とし、説明変数に「駅徒歩（分）」「築年数（年）」「面積（㎡）」の 3 つを使用します。

データの確認

データに関しては目視にて明らかな外れ値は抜いてあります。（これは厳密にはまだ外れ値として省けるものがある余地が残っていることも意味します）

データを読み込んでざっと統計量を確認します。

import pandas as pd
import numpy as np

# データ読み込み
df = pd.read_csv('./data/cleansed.csv')

# 出力数値は小数点第四位まで
pd.options.display.float_format = '{:.4f}'.format

# 統計量
df.describe()

2704 件のデータ
データの範囲（min 〜 max）
- 家賃：30,000 〜 298,000
- 駅徒歩：1 〜 19
- 築年数：1 〜 49
- 面積：7 〜 79.62

説明変数候補に対してサンプルサイズも十分にあるのでこの部分は問題ないと判断できそうです。（過学習回避のためサンプルサイズは説明変数の数に対してその 10 倍以上は欲しい）

目的変数、説明変数のデータの状態を確認

それぞれのデータについて度数分布表とヒストグラムを作成しデータの内容を確認しておきます。

ヒストグラムの描画と度数分布表データを出力する関数を作って各データに当てていきます。

# 関数を定義
def frequency_distribution_table(data, min, max, class_range):
    """度数分布出力

    度数分布表とヒストグラムを出力する.

    Args:
        data (Series): 対象のデータ
        min (int): 階級の最小値
        max (int): 階級の最大値
        class_range (int): 階級幅

    Returns:
        DataFrame: 度数分布表

    """

    scores = pd.Series(np.around(data))

    bins = np.linspace(min, max, class_range)

    freq = scores.value_counts(bins=bins, sort=False)

    class_value = (bins[:-1] + bins[1:]) / 2
    rel_freq = freq / scores.count()
    cum_freq = freq.cumsum()
    rel_cum_freq = rel_freq.cumsum()
    
    dist = pd.DataFrame(
        {
            "階級値": class_value,
            "度数": freq,
            "相対度数": rel_freq,
            "累積度数": cum_freq,
            "相対累積度数": rel_cum_freq,
        },
        index=freq.index
    )
    
    dist.plot.bar(x="階級値", y="度数", width=1, ec="k", lw=2)
    return dist

それぞれの変数ごとに度数分布表とヒストグラムを出力します。

frequency_distribution_table(df['家賃'], 30000, 300000, 16)
frequency_distribution_table(df['駅徒歩'], 1, 20, 16)
frequency_distribution_table(df['築年数'], 1, 50, 16)
frequency_distribution_table(df['面積'], 1, 80, 10)

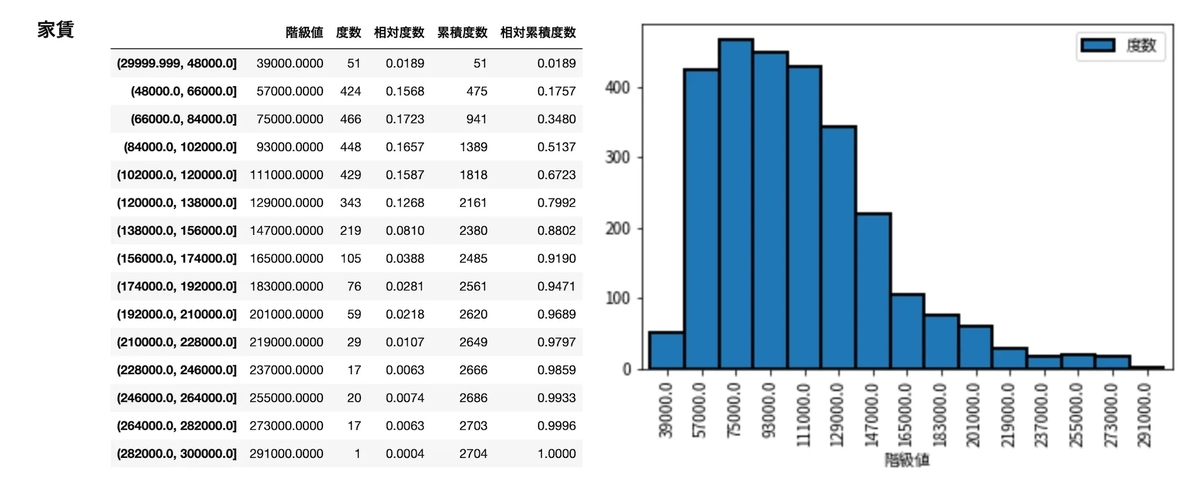
家賃 20 万超えが全体の 3 - 4% くらいしかないのが気になります。

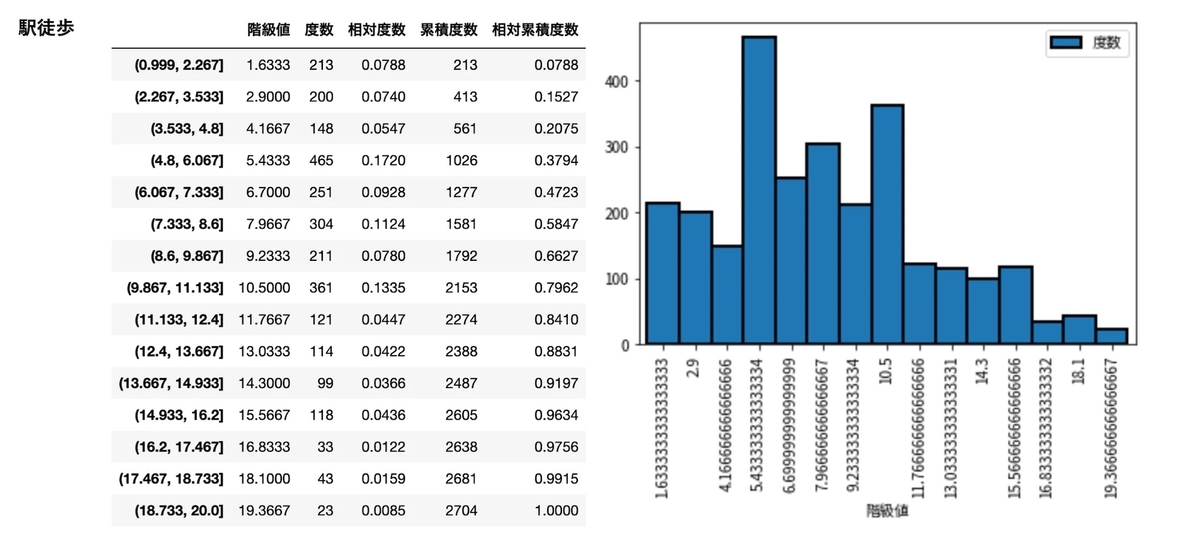
ふたこぶになっているのって、その地域の住宅が多いエリア的なところも起因するのでしょうか。

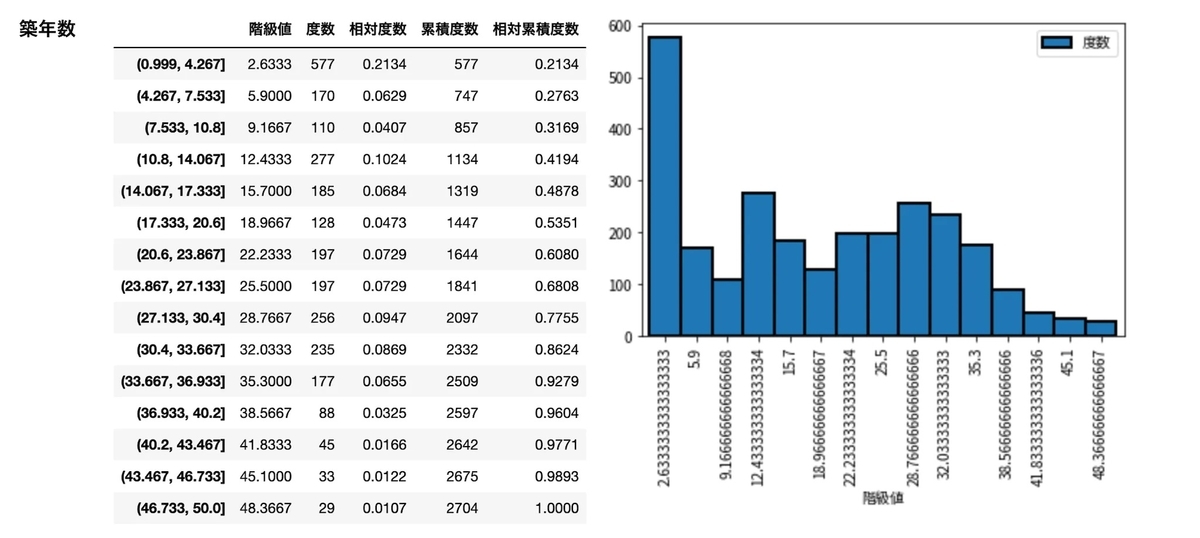
新築・築浅が多いようだけど本当ですかという気持ちにはなる。

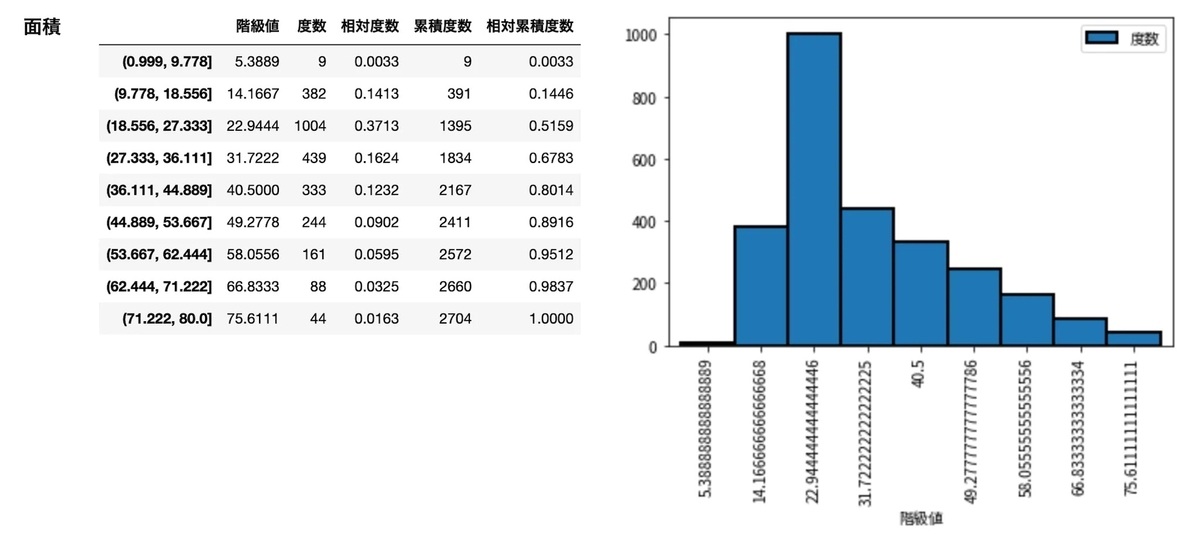
この分布だと結構単身者向けの物件が多そうに見えますね。

と、こんなふうに与えられたデータを眺めるのは大事（明らかな外れ値なども見つけられる）なので必ずデータの状態を確認します。（家賃 20 万超は結局省かずに進めます）

目的変数と各説明変数の相関を確認

次に、散布図と相関係数から、目的変数と各説明変数がどのような関係にあるのかを確認しておきます。

# 説明変数
X = df[['駅徒歩']]

# 目的変数
Y = df[['家賃']]

# 散布図描画
plt.scatter(X, Y)

print("【相関係数 家賃 × 駅徒歩】 ", df['家賃'].corr(df['駅徒歩']))

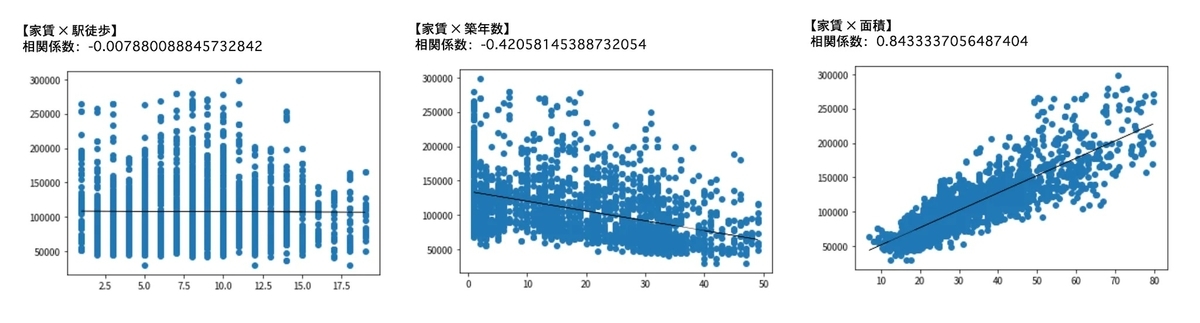
相関係数家賃 × 駅徒歩 = -0.007880088845732842 -> ほとんど相関なし
相関係数家賃 × 築年数 = -0.42058145388732054 -> 弱い負の相関
相関係数家賃 × 面積 = 0.8433337056487404 -> 強い正の相関

面積は大きいほど家賃が上がる傾向にあり、築年数が大きいほど家賃は緩やかに下がる傾向、そして駅徒歩は無相関。

駅徒歩に関しては住宅エリアの文脈もちらつくため一概に距離だけで相関しなさそうという部分もありつつだったので、概ね予想通りの相関関係。

説明変数同士の相関関係を確認

最後に、説明変数同士の相関関係を確認しておきます。

後述する「多重共線性」の確認に先駆けて、説明変数同士の相関関係（互いに無相関であること）を確認しておきます。

Pandas の corr() メソッドで列同士の相関係数（列のペアワイズ相関）を出力します。

df.corr()

また、視覚的に捉えやすいようにヒートマップでも出力します。

import seaborn as sns
 
sns.heatmap(df.corr(), cmap='coolwarm', vmin=-1, vmax=1, annot=True)
plt.show()

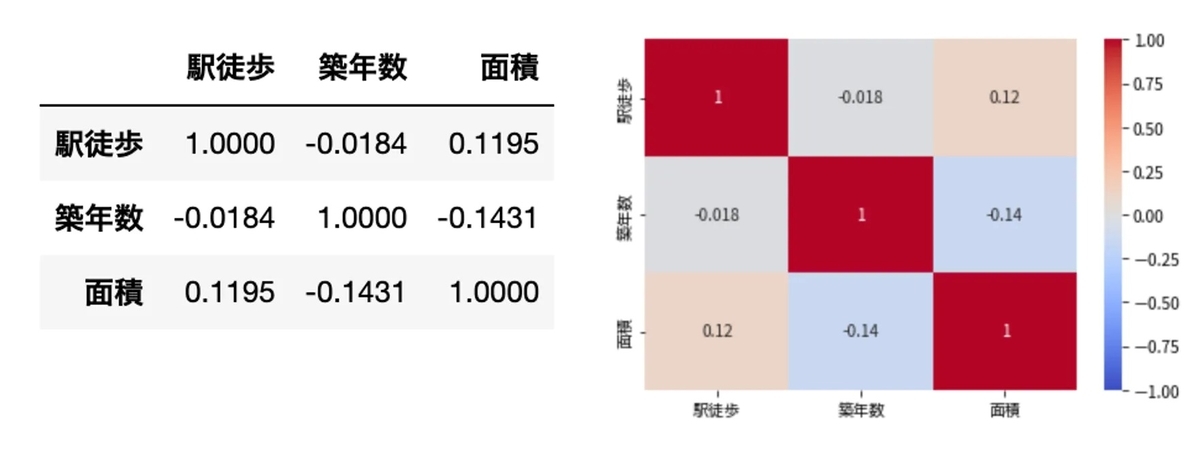
駅徒歩 × 築年数 = -0.0184 -> ほとんど相関なし
駅徒歩 × 面積 = 0.1195 -> ほとんど相関なし
築年数 × 駅徒歩 = -0.0184 -> ほとんど相関なし
築年数 × 面積 = -0.1431 -> ほとんど相関なし

説明変数間の相関はないといえそうです。ペアプロット図（各説明変数間の散布図行列）も描画して確認しておきます。

plt.figure(figsize=(10,10))
sns.pairplot(df, height=2.5)

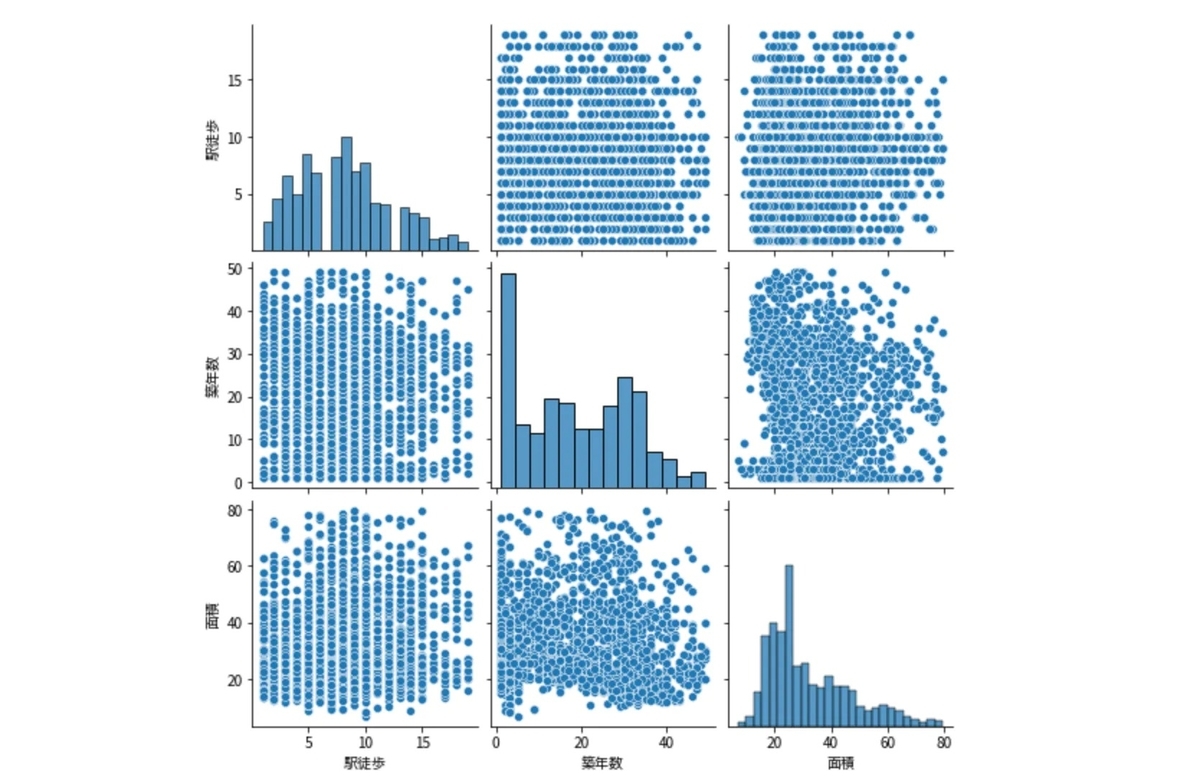
散布図からも無相関であることが読み取れました。

モデル作成

データの確認ができたところで重回帰モデルを作成していきます。

「駅徒歩（分）」「築年数（年）」「面積（㎡）」から「家賃」を推定するモデル
最小二乗法 (Ordinary Least Squares, OLS)を用いる

scikit-learn 重回帰モデル作成

scikit-learn を使って重回帰モデルを作成します。

データは「訓練（トレーニング）用」と「テスト用」とに分割します。訓練用データを使って学習、モデルを作成し、そこで得られた係数をもとに、テスト用データを入れて正確性を求めていきます。

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, mean_squared_error

lr = LinearRegression()

# 説明変数
X = df.drop("家賃", axis=1).values
 
# 目的変数
Y = df['家賃'].values

# テスト用とデータを分割
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=20)

# 予測モデル作成
lr.fit(X_train, y_train)
 
# 偏回帰係数
coef = pd.DataFrame({"Name":df_except_rent.columns, "Coefficients":lr.coef_}).sort_values(by='Coefficients')

# 偏回帰係数
print("【偏回帰係数】", coef)
 
# 切片 (誤差)
print("切片:", lr.intercept_)

# 決定係数（トレーニングデータ）
print("決定係数(訓練):", lr.score(X_train, y_train))

# 決定係数（テストデータ）
print("決定係数(テスト):", lr.score(X_test, y_test))

【偏回帰係数】	Name	Coefficients
0	駅徒歩	-1161.8554
1	築年数	-1058.4004
2	面積	2465.4881

切片: 57907.584454302894
決定係数(訓練): 0.8139363274157336
決定係数(テスト): 0.8166942096869665

statsmodels 重回帰モデル作成

statsmodels でも重回帰モデルを作成します。

（モデル作成において scikit-learn と両方用いる必要はないですが、statsmodels の summary が結構重宝するのでこちらでも作成します。）

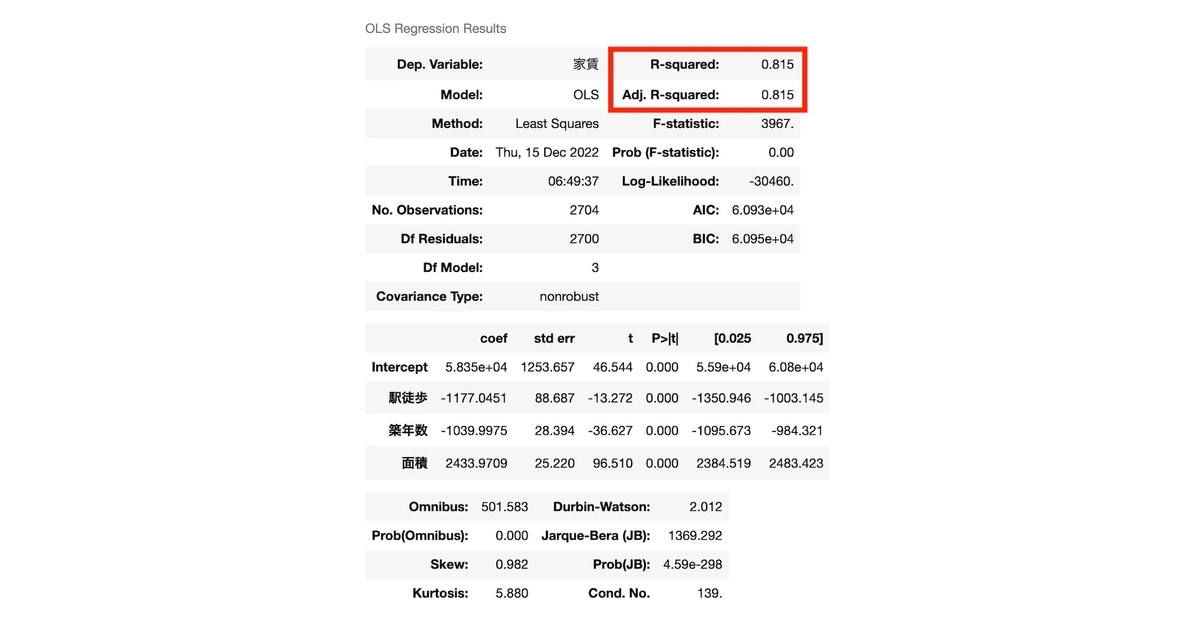
from statsmodels.formula.api import ols

formula = '家賃 ~ 駅徒歩 + 築年数 + 面積'

res = ols(formula, data=df).fit()
res.summary()

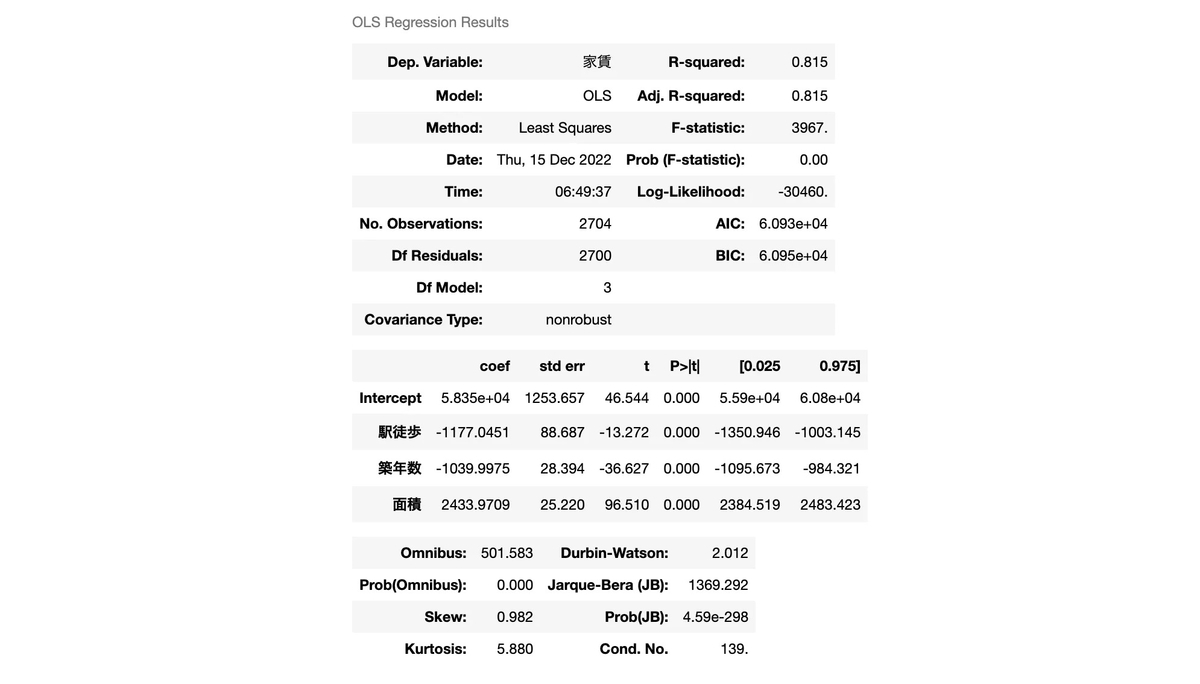
結果確認

それぞれでモデルを作成しました。（数値に関しては scikit-learn と statsmodels で大きな差は無く、statsmodels 側は訓練用・テスト用で分けていないのでそこの誤差程度と思われるため両者を比べることはしません。）

回帰式としては以下が導き出されたことになります。（数値は scikit-learn の方を採用）

$\displaystyle y = -1161.8554a -1058.4004b + 2465.4881c + 57907.5845$

駅徒歩が 1 分増えれば家賃は 1162 円減り、築年数が 1 年増えれば家賃は 1058 円減り、面積が 1㎡増えれば家賃は 2465 円増える。というイメージ。

訓練用、テスト用ともに決定係数は 0.81 と高め。およそ 81% の目的変数を説明できていることにはなります。

ではこのモデルを使って家賃を推定してみます。テスト用データからランダムに抽出したものを使って出力します。

パラメータ	予測された家賃	実際の家賃	残差
駅徒歩: 8.0 築年数: 41.0 面積: 15.3	42940	42000	-940
駅徒歩: 13.0 築年数: 31.0 面積: 18.63	55925	53000	-2925
駅徒歩: 7.0 築年数: 3.0 面積: 9.38	69726	56000	-13726
駅徒歩: 7.0 築年数: 29.0 面積: 18.63	65013	60000	-5013
駅徒歩: 12.0 築年数: 30.0 面積: 17.82	56148	61000	4852
駅徒歩: 7.0 築年数: 29.0 面積: 16.57	59934	61000	1066
駅徒歩: 12.0 築年数: 35.0 面積: 21.41	59707	68000	8293
駅徒歩: 14.0 築年数: 23.0 面積: 23.4	74991	75000	9
駅徒歩: 8.0 築年数: 17.0 面積: 22.0	84861	77000	-7861
駅徒歩: 12.0 築年数: 26.0 面積: 24.2	76112	81000	4888
駅徒歩: 11.0 築年数: 3.0 面積: 19.16	89191	86000	-3191
駅徒歩: 9.0 築年数: 1.0 面積: 18.87	92916	90000	-2916
駅徒歩: 5.0 築年数: 14.0 面積: 24.0	96452	96000	-452
駅徒歩: 12.0 築年数: 14.0 面積: 28.4	99168	101000	1832
駅徒歩: 11.0 築年数: 31.0 面積: 52.2	141015	118000	-23015
駅徒歩: 14.0 築年数: 45.0 面積: 52.8	124191	120000	-4191
駅徒歩: 8.0 築年数: 22.0 面積: 42.9	131097	133000	1903
駅徒歩: 4.0 築年数: 14.0 面積: 46.75	153704	150000	-3704
駅徒歩: 2.0 築年数: 1.0 面積: 45.42	166508	170000	3492
駅徒歩: 10.0 築年数: 12.0 面積: 57.56	175502	185000	9498
駅徒歩: 8.0 築年数: 1.0 面積: 55.24	183748	206000	22252

予測値が近いものは近いけど、遠い時もある。

家賃推定としてどこまでの精度を求めるかによっても、この回帰式が使えるものかどうかは変わりそうです。

家賃 20 万の物件の誤差が 1, 2 万あってもなんとなく許容できそうだけど、家賃 5, 6 万の推定誤差が 5000, 10000 とかだと結構つらいですよね。

ということで、次でこのモデルの検査・評価を行なっていきます。

モデル検査

作成したモデルを検査・評価していきます。

重回帰分析として成立しているか
前提・仮定が満たせているか

などを評価することで、分析自体（手法の選択）に誤りがないかや、精度は十分か、どこが改善できるかなどを見ていきます。

多重共線性の確認

重回帰分析を行う前提として「独立変数間は相互独立（無相関）である」という仮定があります。

独立変数間で関連性が高い（相関がある）状態の場合、回帰係数のバラツキが大きく（標準誤差が大きく）なり、有意な関係が得られなくなってしまうため、有効な回帰式（推定結果）を得られなくなってしまいます。

つまりモデルの精度が落ちることになります。

例）価格（目的変数）・重量（説明変数）・容量（説明変数）の場合

重量と容量には正の相関関係がある＝似たような説明変数になる -> 多重共線性が発生する

この状態のことを 多重共線性（= Multicollinearity, マルチコリニアリティ, 通称：マルチコ） といいます。

統計学において、多重共線性（たじゅうきょうせんせい、英語: Multicollinearity、単に共線性とも略される）とは、重回帰モデルにおいて、説明変数の中に、相関係数が高い組み合わせがあることをいう（例: 体重とBMI）。重回帰分析の際、説明変数を増やすほど決定係数が高くなりやすいために、より多くの説明変数を入れ、多重共線性を起こす可能性がある。このような状況では、モデルやデータの小さな変化に応じて、重回帰の係数推定値が不規則に変化しうる。多重共線性は、少なくともサンプルデータセット内では、全体としてのモデルの予測力または信頼性を低下させず、個々の予測変数に関する計算にのみ影響を与える。つまり、共線性予測変数を持つ多変量回帰モデルは、予測変数の全体がどれだけよく結果変数を予測するかを示すことができるが、個々の予測変数に関する有効な結果、またはどの予測変数が不要かに関しては有効な結果を与えないことも考えられる。
多重共線性 - wikipedia

多重共線性参考

この多重共線性がまず無いことを確認し、重回帰分析として成立しているかを確認します。

説明変数同士の相関関係

これについては「説明変数同士の相関関係を確認」で確認した通り、今回の説明変数間の相関はすべて無相関でした。

VIF による共線性確認

最小二乗法での回帰分析における多重共線性の存在確認として VIF（Variance Inflation Factor, 分散拡大要因） という独立変数間の多重共線性を検出するための指標を確認します。

統計学における分散拡大係数(variance inflation factor, VIF) とは、最小二乗回帰分析における多重共線性の深刻さを定量化する。推定された回帰係数の分散(推定値の標準偏差の平方)が、多重共線性のためにどれだけ増加したかを測る指標を提供する。
分散拡大係数 - wikipedia

独立変数間の相関係数行列の逆行列の対角要素であり、値が大きい場合はその変数を分析から除いた方がよいと考えられる。10を基準とすることが多い。
VIF - 統計 WEB

VIF の求め方

個々の説明変数間の相関係数を求める
それらの相関係数の行列の逆行列を求める
その時の対角要素の値が VIF になる

VIF は１つの説明変数 $x_1$ を目的変数とした他の説明変数による重回帰分析での重相関係数 $r_i$ を用いて以下のように定義される。（VIFは説明変数間ごとに算出する）

$\displaystyle VIF_i = \frac{1}{1 - r^2_i}$

一般に、 VIF の値が 10 を超えると多重共線性の問題があると言われているため、ここの指標を確認します。

多重共線性の基準としてVIF>10が目安になります．VIF>10の場合に説明変数間に多重共線性があると判定を行います．VIF=10は相関係数で換算すると約0.95であり，2変数の関連性が非常に強いこと意味します．
VIF（分散拡大要因） - Stat

python においては statsmodels の variance_inflation_factor を使って VIF 統計量を算出できます。

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif = pd.DataFrame()
vif["VIF"] = [variance_inflation_factor(X_train, i) for i in range(X_train.shape[1])]
vif["features"] = ['駅徒歩', '築年数', '面積']

vif

	VIF	features
0	3.6003	駅徒歩
1	2.2837	築年数
2	3.5255	面積

すべての説明変数において VIF が 5 以下のため、多重共線性は無いと判断できそうです。

偏回帰係数と相関係数の符号の確認

多重共線性の可能性を見るため、併せて偏回帰係数と相関係数の符号を確認しておくのも方法の 1 つです。

多重共線性が見られる場合、ここの符号が逆転する場合があります。

モデルの学習によって導き出された回帰式の各説明変数における偏回帰係数と、目的変数と各説明変数との相関係数の符号が一致していることを確認します。

	偏回帰係数	目的変数との相関係数
駅徒歩	-1161.855	-0.008
築年数	-1058.400	-0.421
面積	2465.488	0.843

各符号が一致していることを確認できました。

多重共線性が見られる場合の対応

多重共線性が確認できる場合は、共線性にある説明変数の片方を回帰式から取り除きます。　

残差分析

重回帰分析で残差が満たされるべき仮定である以下 3 つを確認します。

独立性
等分散性
正規性

1. 独立性

仮定：各独立変数の残差間に相関がない（データそれぞれが独立である）こと。

ダービン・ワトソン検定で確認でき、0 〜 4 までの値をとり、この値が 2 に近いほどよいと言われている。

ダービン・ワトソン比（Durbin-Watson ratio, DW比）

誤差項（実測値と理論値の差）間に自己相関があるかないかを判別するための指標。回帰分析では、異なる誤差項間には相関がないことを仮定しているため、ダービン=ワトソン比がその指標となる。

値が2よりかなり小さいときは正の相関が、2よりかなり大きいときは負の相関が、2前後のときは相関なしと判断する。
ダービン=ワトソン比 - 統計 WEB

ダービン・ワトソン比は statsmodels.summary で算出されるため、そこから値を確認できます。

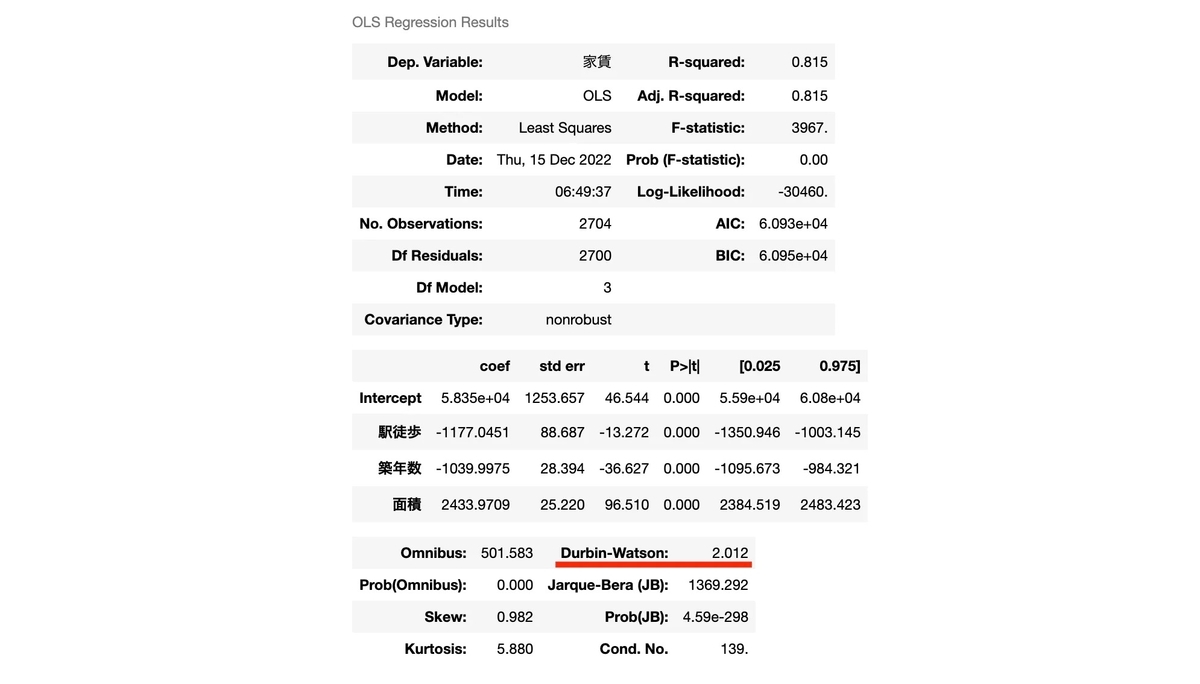
Durbin-Watson: 2.012

そのため自己相関はなしと判断、独立性は満たされたといえます。

2. 等分散性

仮定：説明変数がどの値のときも残差の分散が一定である。

予測した回帰直線に対して、残差が一定（0を中心に均一）の散らばり具合であることが望ましいとされている。

残差プロットによる可視化

モデルの回帰直線に対して残差をプロットし、散らばり具合を目視で確認してみます。

# 予測値（学習データ）
y_train_pred = lr.predict(X_train)

# 予測値（テストデータ)
y_test_pred  = lr.predict(X_test)

# 残差（学習データ）
residual_error_train = y_train - y_train_pred

# 残差（テストデータ）
residual_error_test = y_test - y_test_pred,

# 予測値と残差をプロット（学習データ）
plt.scatter(y_train_pred, residual_error_train, c='blue', marker='o', s=40, alpha=0.7, label='学習データ')

# 予測値と残差をプロット（テストデータ）
plt.scatter(y_test_pred, residual_error_test, c='red', marker='o', s=40, alpha=0.7, label='テストデータ')

plt.xlabel('予測値')
plt.ylabel('残差')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-50000, xmax=300000, lw=2, color='black')
plt.xlim([-50000, 300000])
plt.ylim([-120000, 100000])
plt.tight_layout()
plt.show()

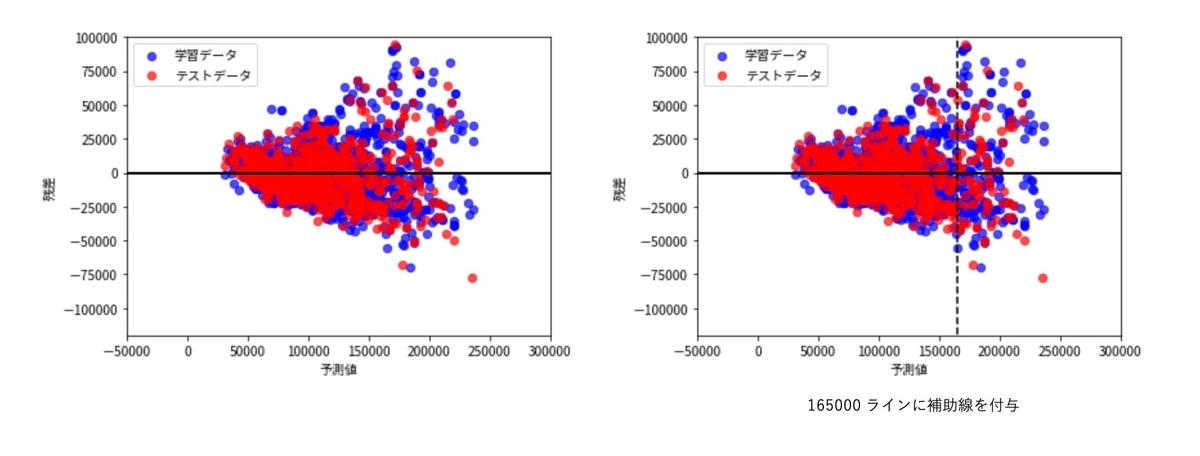
2 つのプロットは同じものですが、右側は x=165000 で補助線を引いています。

予測値が 165000 を超えたあたりから残差にぱらつきが出始めています。

家賃 165000 以上のデータを確認すると、全体の 9% 未満のため、このレンジに関しては回帰モデルが目的変数を説明できるほど学習できていない可能性はありそうです。

また、今回の傾向は予測が大きくなるに従って残差が大きくなる「分散不均一性」を示しています。

分散不均一性

そもそも「分散均一性（homoscedasticity）」とは「モデルの誤差が一様に分布している」ことを指しますが、

今回の「分散不均一性（heterogeneity）」はその逆で、「モデルの誤差が一様に分布していない」ことを指します。

今回の結果で言えば「x が増えるにつれて y の分散が大きくなってしまっている」という状態です。

この「分散不均一性」という状態を今回の残差プロットから解釈すると、家賃が安い場合は、その賃料を決定するための要素として「駅徒歩」「築年数」「面積」以外が入る余地はあまりあるわけではないが、家賃が高い場合、これら 3 要素以外の家賃決定の要素が安い場合よりも多く寄与していることで推定にばらつきが出ている。と考えられます。

この、「家賃が高い賃貸物件ほど残差のばらつきが大きくなる」は、推定したい賃料が上がることで、説明変数で説明できない部分が大きくなっている。

ということを示しています。

先ほど、ばらつきが顕著に出始めた家賃 165000 以上のデータが全体の 9% 未満であると言いましたが、分散不均一性が見て取れるということは、

「学習データを増やしてもモデルの精度は上がらない」

ということになるのでしょうか。（ここにおける当たり前を知らないのでぜひ試してみたい）

今回、分散不均一性が見られたことから、このモデルの精度をもっと上げるためには「説明変数の追加を検討する」という一つの考察が得られました。

3. 正規性

仮定：誤差は正規分布している

重回帰分析では、残差が正規分布しているという仮定を満たしたいため、正規性を確認していきます。

ヒストグラムによる確認

まずは残差のヒストグラムを作成し確認します。

# 学習データでの残差（残差 = 観測値 –予測値）
y_train_residual_error = y_train - y_train_pred

# テストデータでの残差
y_test_residual_error =  y_test - y_test_pred

# ヒストグラムにプロット
frequency_distribution_table(y_train_residual_error, -100000, 100000, 30)
frequency_distribution_table(y_test_residual_error, -100000, 100000, 30)

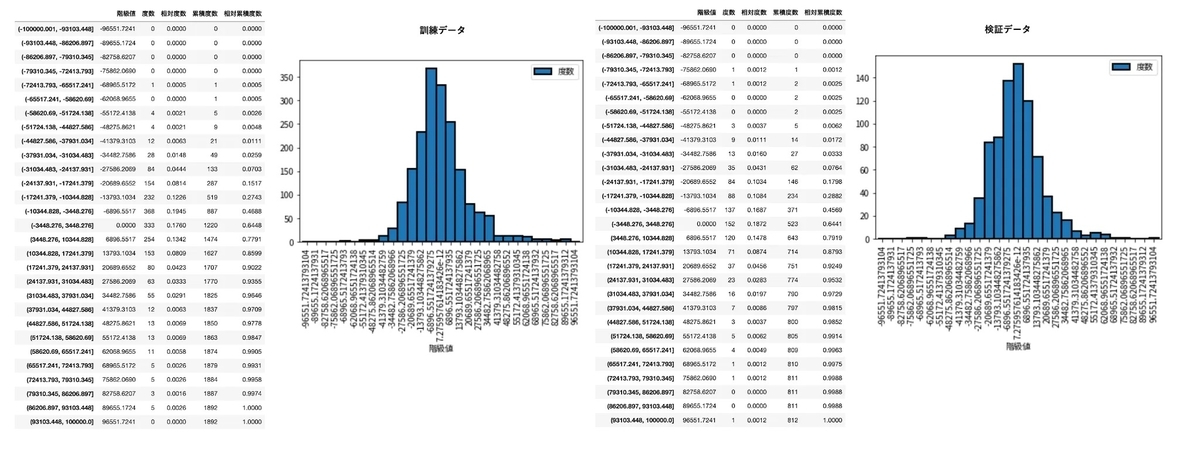
だいたい正規分布の形にはなっているので、正規性は満たされているといえそうです。

正規 Q-Q プロットによる確認

ヒストグラム以外でも正規性を確認しておきます。

誤差が正規分布していることを Q-Q プロット（Quantile-Quantile plot）でも確認します。

正規Q-Qプロット

normal Q-Q plot

観測値が正規分布に従う場合の期待値をY軸にとり、観測値そのものをX軸にとった確率プロット。

観測値を昇順に並べた順位からパーセンタイル（累積確率）を求め、正規分布の確率密度関数の逆関数を用いて期待値を予測する。プロットが一直線上に並べば、観測値は正規分布に従っていると考えられる。
正規Q-Qプロット - 統計 WEB

statsmodels の qqplot を用います。

import statsmodels.api as sm

sm.qqplot(y_test_residual_error, fit=True, line='45')

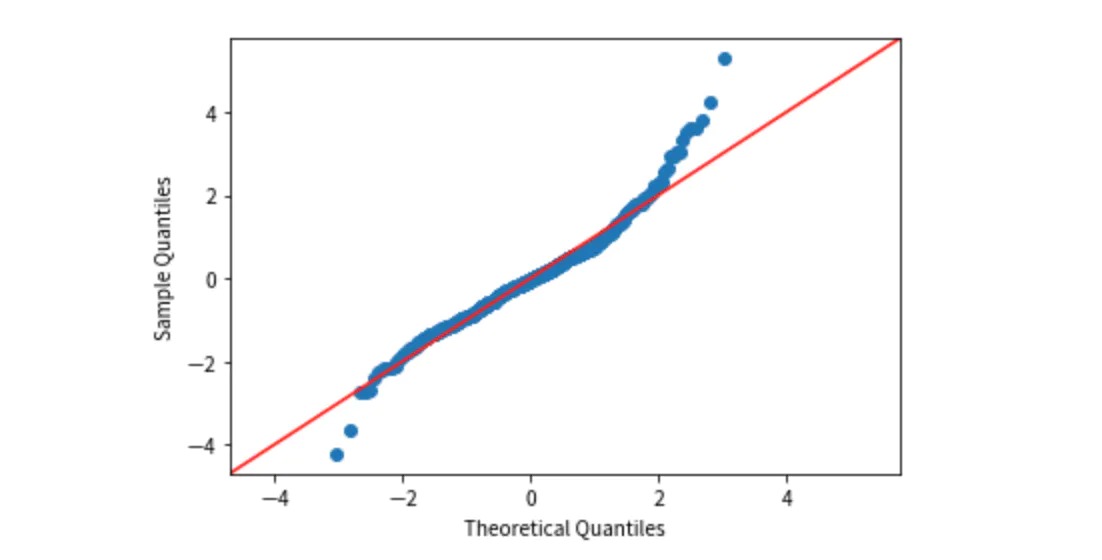
右上の方が少し外れてはいますが、おおよそ直線上には乗っているので、正規性について概ね満たされているといえそうです。

モデル精度評価

回帰分析は入力 $x$ に対して出力 $y$ を得ることのできるもの。そのためモデルの精度を評価するためには出力の実測値を予測値がどれくらい再現できているかを検証する必要がある。

以下で回帰分析におけるモデルの精度を評価していきます。

決定係数（R-Squared, $R^2$ ）

決定係数とは、推定された回帰式の当てはまりの良さを表す指標のこと。

0 から 1 までの値を取り、1 に近いほど回帰式の当てはまりが良いことを示す。（説明変数が目的変数をよく説明できている）

ただし「決定係数の値がどれくらいであれば精度が良い」というのは統計学的な基準は無く、ケースバイケース、経験的な部分での判断になっている。

（とはいえ、一般には以下が多いか）

$R^2$ の値	精度評価
$R^2 \geqq 0.8$	良い
$R^2 \geqq 0.5$	やや良い
$R^2 \lt 0.5$	良くない

決定係数は一般に $R^2$ と表し、以下の式で求める。

$\displaystyle R^2 = 1 - \frac { \sum_{i=1}^{n}(y_i - \hat{y_i})^2 } { \sum_{i=1}^{n}(y_i - \bar{y})^2 }$

$y_i$ ：観測値 $(i = 1,2, ..., n)$
$\hat{y_i}$ ：予測値
$\bar{y}$ ：観測値の平均

$\displaystyle R^2 = 1 - \frac{残差の変動（目的変数の予測値の偏差平方和）}{全体の変動（目的変数の観測値の偏差平方和）}$

計算式の深堀りは次の機会として、scikit-learn で算出してみます。

from sklearn.metrics import r2_score

# 予測値(訓練データ）
y_train_pred = lr.predict(X_train)

# 予測値（検証データ)
y_test_pred  = lr.predict(X_test)

r2_train = r2_score(y_train, y_train_pred)
r2_test  = r2_score(y_test, y_test_pred)

r2_train, r2_train

決定係数
- 訓練データ: 0.8139
- 検証データ: 0.8139

決定係数は 0.8139 で基準とした 0.5 を大きく上回ったので、この回帰式は予測に使えると断定、、はできないですが、「予測の当てはまりの良さ」は概ね良さそうではある。と判断はできそうです。

なぜ決定係数だけでモデルの精度の良さを判断できないのかは検索すればたくさん出てきますが、今回の場合は分散不均一性が出ており、高めの家賃における精度がいまいちなのが明瞭であることもあります。

ここの数値が高くてもモデルの検査は必要ですし、数値として低くないことを確認できれば良しかなと思います。

自由度調整済み決定係数(adjusted R-Squared, $R^2_f$ )

決定係数には、たとえ無意味な変数であっても「変数の数が多ければ多いほど値が高くなる」という性質があるため、決定係数よりも、その欠点を補った「自由度調整済み決定係数」を見ていくことが多い。

$\displaystyle R^2_f = 1 - \frac{SS_e}{SS_y} × \frac{n-1}{n-p-1}$

$\displaystyle R^2_f = 1 - 決定係数 × \frac{サンプルサイズ - 1}{サンプルサイズ - 説明変数の数 - 1}$

自由度調整済み決定係数は scikit-learn に用意されていないので、関数を作成して求めてみます。

from sklearn.metrics import r2_score

def adjusted_r2_score(y_actual, y_pred, number_dimensions):
    """自由度調整済み決定係数出力

    Args:
        y_actual (ndarray): 観察データ
        y_pred (ndarray): 予測データ
        number_dimensions (int): 次元数（説明変数の数）

    Returns:
        float: 自由度調整済み決定係数
    """
    # 決定係数
    coefficient_of_determination = r2_score(y_actual, y_pred)
    # サンプルサイズ
    sample_size = len(y_actual)
    
    return 1 - (1 - coefficient_of_determination) * (sample_size - 1) / (sample_size - number_dimensions - 1)

# 訓練データ
adj_r2_score(y_train, y_train_pred, X_train.shape[1])
# 検証データ
adj_r2_score(y_test, y_test_pred, X_test.shape[1])

自由度調整済み決定係数
- 訓練データ: 0.8136
- 検証データ: 0.8160

自由度調整済み決定係数は、決定係数に対して、説明変数の数に応じたペナルティを与えた係数になるため、基本的には決定係数に比べて数値が下がる傾向にあります。

算出した決定係数と自由度調整済み決定係数を比べてみます。

	次元数	サンプルサイズ	決定係数	自由度調整済み決定係数
訓練データ	3	1892	0.8139	0.8136
検証データ	3	812	0.8139	0.8160

今回の場合は説明変数 3 に対してサンプルサイズもそこそこ多いため、大きなペナルティはなかったようです。双方ほぼ変わりませんでした。

ちなみに決定係数、および自由度調整済み決定係数については、statsmodels summary でも算出されるので、そこで確認もできる。

自由度調整済み決定係数についても、数値に対する判断は決定係数と変わらないため、数値として低くないことを確認できれば良しと思います。

MSE（Mean Squared Error, 平均二乗誤差）

MSE は残差の二乗の平均。モデルの精度の悪さがわかる。

「実際の値と線形回帰モデルによる予測値のズレ（誤差）がどれだけあるか」が算出される。

MSE を評価関数として利用する場合、出力値は 0 に近いほど良いと評価する。

$\displaystyle MSE = \frac{1}{n} \sum_{i=1}^{n}(\hat{y_i} - y_i)^2$

$\displaystyle MSE = \frac{1}{サンプルサイズ} \sum_{i=1}^{n}(予測値_i - 実測値_i)^2$

最小二乗法による線形回帰は訓練データの MSE が最小になるようにパラメータを学習している。（最も一般的な損失関数）

式から1/nを外すと（＝総和だけで平均しない場合）、「二乗したL2ノルム（ユークリッド距離）」（＝平方根√しないL2ノルム）の式と同じになる。二乗したL2ノルムや、それに1/2を掛けたものは、L2損失（L2 Loss）とも呼ばれる。
［損失関数／評価関数］平均二乗誤差（MSE：Mean Squared Error）／RMSE（MSEの平方根）とは？ - @IT

MSE は二乗している関係で、指標そのものがわかりにくいという面があります。

そのため、MSE を算出する前に次の RMSE を見ておきます。

RMSE（Root Mean Squared Error, 二乗平均平方根誤差）

RMSE は、MSE で二乗したことの影響を平方根で補正した指標。MSE で二乗した単位が元に戻るため MSE よりもわかりやすいと言われる。

$\displaystyle RMSE = \sqrt{ \frac{1}{n} \sum_{i=1}^{n}(\hat{y_i} - y_i)^2 }$

こちらも MSE 同様、値が小さければ小さいほどよいという指標になる。

では、scikit-learn の mean_squared_error を使って MSE と RMSE を算出してみます。

from sklearn.metrics import mean_squared_error

print('MSE 訓練: %.4f, テスト: %.4f' % (
        mean_squared_error(y_train, y_train_pred, squared=True),
        mean_squared_error(y_test, y_test_pred, squared=True) 
      ))

print('RMSE 訓練: %.4f, テスト: %.4f' % (
        mean_squared_error(y_train, y_train_pred, squared=False),
        mean_squared_error(y_test, y_test_pred, squared=False)
      ))

	訓練データ	テストデータ
MSE	368349364.7368	330385018.0791
RMSE	19192.4299	18176.4963

決して小さくはない、というか家賃推定ではむしろ大きい値かも。

単位的な見方が曖昧なので MSE だと全然わからないですね。RMSE の方がまだわかりやすいです。

MSE や RMSE は「誤差を二乗する」という特性上、誤差が大きいとその分過敏に結果に跳ね返ります。

今回のモデルの性能としてはやはりまだ精度が甘いことがここからわかりました。

学習する上で外れ値がないかの確認を行なって精度を上げていきたいところです。

MAE（Mean Absolute Error, 平均絶対誤差）

MAE は、誤差の絶対値の平均。

$\displaystyle MAE = \frac{1}{n} \sum_{i=1}^{n} |\hat{y_i} - y_i|$

$\displaystyle MAE = \frac{1}{サンプルサイズ} \sum_{i=1}^{n} |予測値_i - 実測値_i|$

シンプルに誤差の平均なので評価指標としては見やすいものかもしれません。

式から1/nを外すと（＝総和だけで平均しない場合）、L1ノルム（マンハッタン距離）の式と同じになる。このことからMAEは、L1損失（L1 Loss）やL1ノルム損失（L1-norm Loss）とも呼ばれる。
［損失関数／評価関数］平均絶対誤差（MAE：Mean Absolute Error）／L1損失（L1 Loss）とは？ - @IT

MAE は、scikit-learn の mean_absolute_error を使って算出できます。

from sklearn.metrics import mean_absolute_error


print('MAE 訓練: %.4f, テスト: %.4f' % (
        mean_absolute_error(y_train, y_train_pred),
        mean_absolute_error(y_test, y_test_pred)
      ))

MAE
- 訓練データ: 13957.4792
- テストデータ: 13447.9865

高額家賃の場合の精度が悪いのもあり、誤差平均はあまりよくありません。

モデルの当てはまりは満足いくほどには高くないということはわかりました。

この指標をみる時は全体として誤差を小さくしたいという観点で見ていくのが良さそうです。

これらの指標はモデルが実データに対してどのくらい当てはまりが良いかを表しています。非常にざっくり言えば、出来たモデルの回帰線と実データの距離がどのくらい近いかを表しています。そのため、未知のデータに対する予測精度を表しているわけでは無いので注意が必要です。
決定係数・MAE・MSE・MRSE - ケイタブログ

たしかにここは混同しないようにしていきたいところ。

AIC（Akaike's Information Criterion, 赤池情報量規準）

一般にパラメータ（説明変数）を増やしていくことでモデルの適合度を高められるが、本当は無関係であるパラメータであってもその変動に合わせてしまう（過学習）ため予測精度が落ちていく。

AIC はこの「モデルの複雑さとデータの適合度とのバランス」を見るための指標であり、「モデルの予測精度」を見るための指標。

値が小さいほど良い。AIC 最小のモデルを選択すれば、多くの場合良いモデルが選択できる。

一方で AIC は相対的な評価として用いるため値の基準（xx 以下だと良い）はなく、現状モデルの値から説明変数の数を調整した際にどう変動したかを見ていくのが良さそうです。

AICの計算式は以下

$\displaystyle \begin{aligned} 定数項あり \\ &AIC = -2log L + 2(k+1) \\ 定数項なし \\ &AIC = -2log L + 2k \end{aligned}$

L：モデルの最大尤度、
k：説明変数の数

赤池情報量規準 - wikipedia によるとAIC の計算式にはいくつか流儀があるらしい。

では AIC を算出してみます。

from math import log, sqrt, pi
from sklearn.metrics import mean_squared_error

def aic(y_actual, y_pred, number_dimensions, has_constant_term=True):
    """AIC 出力

    Args:
        y_actual (ndarray): 観察データ
        y_pred (ndarray): 予測データ
        number_dimensions (int): 次元数（説明変数の数）
        has_constant_term (bool): 定数項の有無 

    Returns:
        float: AIC
    """
    
    # サンプルサイズ
    sample_size = len(y_actual)

    # パラメータ数
    k = number_dimensions + 1 if has_constant_term == True else 0 
    
    # MSE
    mse = mean_squared_error(y_actual, y_pred, squared=True)

    aic = -2 * sample_size * log(1 / sqrt(2 * pi * mse)) + sample_size + k
    
    return aic

aic(y_train, y_train_pred, X_train.shape[1])

AIC: 42692.09764269398

この数値だけだと評価できないので、説明変数を 1 つ減らした（駅徒歩を除去）した場合で AIC を出してみます。

	AIC
説明変数 2 つ	488154.7536
説明変数 3 つ	42692.0976

今回のモデルでは、説明変数 3 つの方が値は小さいため、説明変数は 2 つより 3 つの方が予測精度は高いと見て取れます。

AIC は予測精度の指標ということで、パラメータの数は適切か、どのパラメータを除去するか。の道標になってくれそうです。

結論

重回帰モデルを構築し、モデルを検査、そして精度評価までを行い、以下のことがわかりました。

分析手法として重回帰分析を選択していること、そして現在の説明変数を採用していることに誤りはない。
分散不均一性が見られるため、説明変数の追加を検討
1. ただし、追加できる変数がなければ家賃のレンジを分けてしまうことも選択肢としてはあるかもしれない。
外れ値がある可能性があるので再度データを確認する
1. ただし外れ値と言っても、入力ミスは無い前提でレンジとして少ない割合のものを除外するという判断はどうなのかがまだ不明瞭。

モデルを作成し、検査や精度評価をしっかり実施していくことで、モデルの改善を行うためのヒントが得られました。

このサイクルでモデルを改善し、精度の良い、当てはまりの良いモデルを作り上げていきたいところです。

モデルの改善も、次の機会に行いたいと思います。

現在 back check 開発チームでは一緒に働く仲間を募集中です。 herp.careers herp.careers herp.careers herp.careers https://herp.careers/v1/scouter/-72jPhOMjaG8herp.careers herp.careers